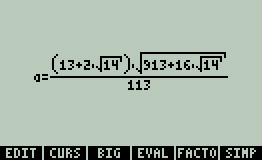La question (de géométrie) du dimanche soir

[dprtl]

Sur ce problème, ma Casio fx-CP400 affichait simplement l'équation de chacun des cercles que j'avais dessinés dans son application Géométrie. Mais ce système de 3 équations du second degré à 3 inconnues était un peu difficile à résoudre. Alors, après le message "désespéré" (un bien grand mot ) de Marge à 2:51 am, j'avoue que j'ai grugé avec la version mobile en ligne de wolframalpha.com sur mon téléphone :

Mathematics -> Algebra -> Polynomials -> Solve a system of polynomial equations



L'ergonomie et la puissance de ce truc sont remarquables. On obtient presque instantanément plusieurs valeurs approchées ou exactes de a (seule la positive m'intéresse ici), ainsi que les coordonnées de E :

[zpalm]

L'ergonomie et la puissance de ce truc sont remarquables.

Stephen Wolfram, le créateur du site est un type particulier: https://blog.stephenwolfram.com/2019/02 ... structure/

[Gilles59]

Sur ce problème, ma Casio fx-CP400 affichait simplement l'équation de chacun des cercles que j'avais dessinés dans son application Géométrie. Mais ce système de 3 équations du second degré à 3 inconnues était un peu difficile à résoudre. Alors, après le message "désespéré" (un bien grand mot ) de Marge à 2:51 am, j'avoue que j'ai grugé avec la version mobile en ligne de wolframalpha.com sur mon téléphone : (…)
L'ergonomie et la puissance de ce truc sont remarquables. On obtient presque instantanément plusieurs valeurs approchées ou exactes de a (seule la positive m'intéresse ici), ainsi que les coordonnées de E :

le CAS de la 50G le résoud également symboliquement. Par contre, curieusement iln'arrive pas à simplifier le résultat sous cette forme et sort une solution identique mais plus complexe. Si je fais la différence des 2, la HP50 ne trouve pas zéro… Ca me rappelle un vieil entretien de B Parisse que j'ai lu quelque part : un des enjeux des CAS c'est de déterminer qu'une expression est égale à zéro.

Je trouve



Wolfram voit de suite que :

sqrt(17+4*sqrt(14))-((13+2*sqrt(14))*sqrt(913+16*sqrt(14)))/113 = 0
Pourtant ce n'est pas du tout évident à l'œil que :

sqrt(17+4*sqrt(14))=((13+2*sqrt(14))*sqrt(913+16*sqrt(14)))/113
La vénérable HP50 n'y arrive pas… sauf à faire x² puis racine carré ….

[C.Ret]

Et si l'on utilise le CAS d'une TI-92, on obtient encore une simplification différente :

QdGdD TI-92 axyd.gif (13.55 Kio) Consulté 3121 fois

Mais je crois que ces différences proviennent plus de la façon de décomposer les trois équations que d'autre chose.


Dans mon cas, x et y sont deux fractions ayant le même dénominateur 2*a et des numérateurs très proches en a²+i où i est un nombre impair (respectivement 9 et 7 pour x et y). Comme a est un radical composé, seul doit apparaitre √14 au numérateur et le 17 s'ajoute au nombre i impair. On peut donc faire disparaitre le facteur 2 du dénominateur car la somme de deux impairs est paire.


Il en résulte naturellement au numérateur 2√14 avec le terme 13 pour x (la moitié de 17+9 = 26) et le terme 12 pour y (la moitié de 17+7 = 24).
Bon d'accord, la TI-92 fait du zèle en factorisant 12+2.√4 qui est réarrangé en 2.(6+√14)

QdGdD TI-92 xyaxy.gif (11.16 Kio) Consulté 3121 fois

J'ai du mal à comprendre les méandres que suivent Wolfram Alpha, HP Prime ou HP-50g. Mais il doit y avoir une bonne raison logique.